Dominio de las líneas numéricas: Una guía completa

A la hora de entender el mundo de las matemáticas, las líneas numéricas desempeñan un papel fundamental. En el ámbito de las matemáticas elementales, la recta numérica es una poderosa herramienta, una representación gráfica de los números reales que proporciona una clara representación visual de las relaciones numéricas. Cada punto de las líneas numéricas corresponde a un número real, mientras que cada número real está representado por un punto de este continuo infinito.

Estas líneas rectas horizontales, divididas uniformemente para representar números enteros, ofrecen una herramienta visual para comprender conceptos numéricos, realizar operaciones aritméticas y mejorar la fluidez matemática general.

Comprender las líneas numéricas

Definición: Las rectas numéricas son líneas rectas horizontales que se utilizan para representar números enteros en un intervalo regular. Sirven de ayuda visual para comprender el concepto de número y su posición relativa. Los números situados a la derecha de la recta numérica son mayores, mientras que los situados a la izquierda son menores.

Las rectas numéricas se extienden infinitamente en ambas direcciones, lo que las convierte en una herramienta versátil para comprender una amplia gama de valores numéricos. Proporcionan una base para comparar, ordenar y realizar operaciones aritméticas con números enteros, fracciones y decimales.

Colocar números en una recta numérica

Para utilizar eficazmente las rectas numéricas, es fundamental saber localizar y representar los números con precisión. El cero sirve como punto medio de una recta numérica, separando los números enteros positivos de los negativos. Los números positivos se sitúan a la derecha del cero, mientras que los negativos se sitúan a la izquierda.

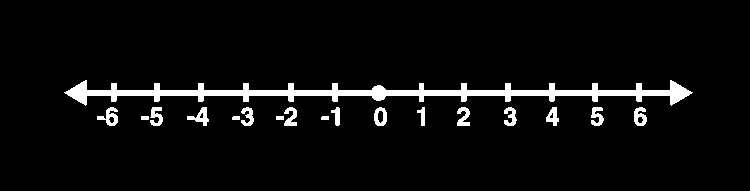
En esencia, una recta numérica es una línea recta graduada. No se limita a mostrar números enteros, sino que abarca todos los números reales y se extiende infinitamente tanto en sentido positivo como negativo. Este carácter inclusivo la convierte en una valiosa ayuda didáctica, sobre todo cuando se introducen conceptos como la suma y la resta, en los que entran en juego los números negativos.

Por ejemplo, consideremos las siguientes comparaciones:

0 es menor que 1
-1 es menor que 0
-2 es menor que -1
Estas sencillas comparaciones ilustran el principio fundamental que rige las líneas numéricas.

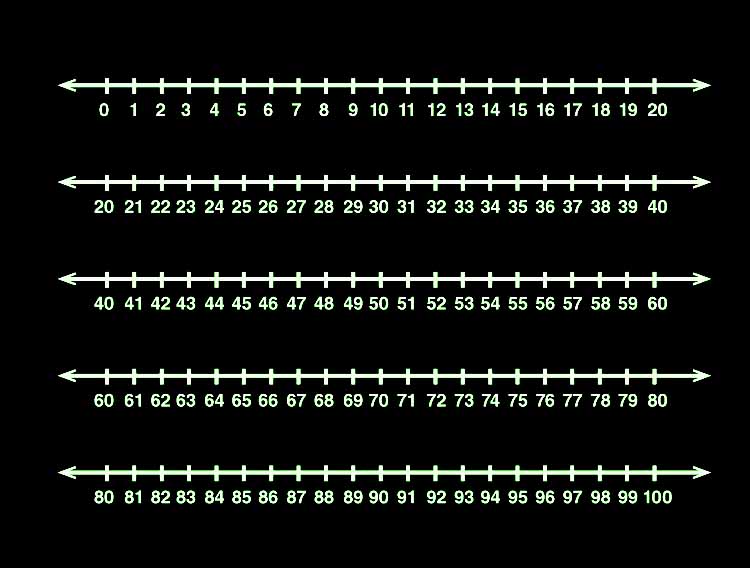
las líneas numéricas pueden extenderse hasta cualquier límite y cualquier tipo de sistema numérico que desee o quiera diseñar. No se limita a la cantidad o al tipo de número. Aquí se muestra una línea numérica de 100.

Perspectivas matemáticas avanzadas

A medida que avanzan las matemáticas, la recta numérica se transforma en la recta real o recta de los números reales, definida formalmente como el conjunto de todos los números reales. Esta transformación implica considerar la recta numérica como un espacio geométrico, concretamente el espacio unidimensional euclidiano, o como un espacio vectorial, un espacio métrico, un espacio topológico, un espacio de medidas o incluso un continuo lineal.

Notación y terminología

En notación matemática, la línea real se denota normalmente con el símbolo “R”, a veces estilizado como “ℝ” en negrita de pizarra. Ocasionalmente, se representa como “R1” o “E1” para enfatizar su papel como primer espacio real o primer espacio euclidiano.

Un vistazo a la historia de las líneas numéricas

La idea de utilizar una recta numérica para las operaciones matemáticas se remonta a siglos atrás. El tratado de álgebra de John Wallis fue uno de los primeros en describir la suma y la resta en una recta numérica, empleando la metáfora de una persona caminando hacia delante y hacia atrás para ilustrar estas operaciones. Aunque existían representaciones anteriores, como la tabla de logaritmos de John Napier, éstas no implicaban explícitamente operaciones.

Operaciones aritméticas en líneas numéricas

Las líneas numéricas ofrecen una plataforma tangible para explicar las operaciones aritméticas. Tanto si se trata de sumar como de restar números, una recta numérica puede ayudar a visualizar el proceso.

Suma en líneas numéricas

Suma de números positivos: Al sumar dos números positivos, el resultado es siempre un número positivo. Para ilustrarlo, sumemos 1 y 5:

• Empieza situando el 1 en la recta numérica.
• Desplázate 5 posiciones hacia la derecha para llegar a 6.

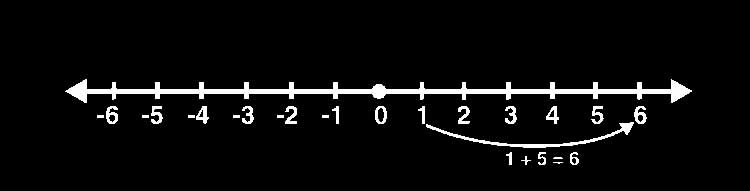
Si quieres saber cómo funciona la suma entra en el siguiente enlace o si necesitas algún truco de suma pincha aquí

Restas en líneas numéricas

Restar números positivos: Al restar un número positivo de otro, desplázate hacia la izquierda por el valor del segundo número. Por ejemplo, restar 5 de 2:

• Empieza encontrando el 2 en la recta numérica.
• Muévete 5 lugares a la izquierda, lo que da como resultado -3.

Suma de números negativos: La suma de dos números negativos produce un resultado negativo. Al sumar -2 y -3

• Localice -2 en la recta numérica.
• Mueve 3 lugares a la izquierda, llegando a -5.

Restar números negativos: Restar un número negativo implica desplazarse hacia la derecha por el valor del segundo número. Por ejemplo, restar -4 de -2:

• Localiza -2 en la recta numérica.
• Muévete 4 lugares a la derecha, llegando a 2.

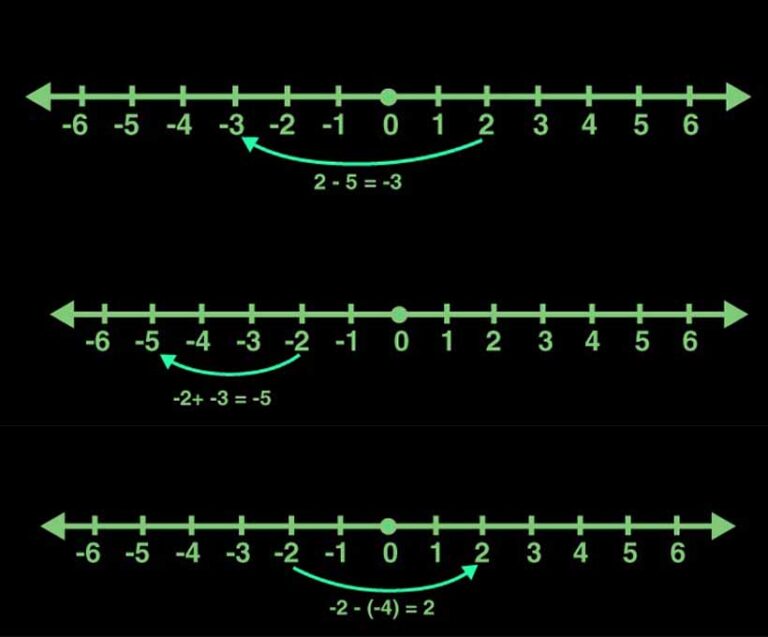
la resta en la recta numérica se muestra según el orden ascendente para saber más sobre la resta ve a esta página o para conseguir algunos trucos sobre la resta pulsa aquí

Conclusión

ConclusiónEn el ámbito de las matemáticas, las líneas numéricas son una herramienta indispensable para comprender los números, sus relaciones y realizar operaciones aritméticas. Tanto si eres un estudiante que busca mejorar sus habilidades matemáticas como si eres un educador en busca de recursos didácticos eficaces, dominar las líneas numéricas es un paso crucial hacia el dominio de las matemáticas. Explore el mundo de los números a través de la claridad visual y la simplicidad lógica de las líneas numéricas, y libere el potencial del dominio matemático.