¿Te has preguntado alguna vez cómo entienden los ordenadores y los smartphones nuestra forma de comunicarnos? Todo se debe a los sistemas numéricos. El lenguaje con el que está construido un ordenador o un móvil es binario, y forma parte de los sistemas numéricos.
Los sistemas numéricos sirven de base sobre la que se construyen todos los cálculos y operaciones matemáticas. Estos sistemas nos proporcionan los medios para representar y manipular los números de forma eficiente. Los sistemas numéricos desempeñan un papel fundamental en una amplia gama de cálculos matemáticos, desde complejos cálculos científicos hasta tareas cotidianas.
este articulo es sobre el sistema numérico si quieres saber sobre los tipos de números puedes leer esto.
Comprender los sistemas numéricos
Un sistema numérico, en su esencia, es una forma sistemática de representar números utilizando reglas y símbolos predefinidos. Es el lenguaje de las matemáticas, que nos permite transmitir cantidades, realizar cálculos y resolver problemas complejos. Profundicemos en los entresijos de los distintos sistemas numéricos.
Sistema numérico decimal
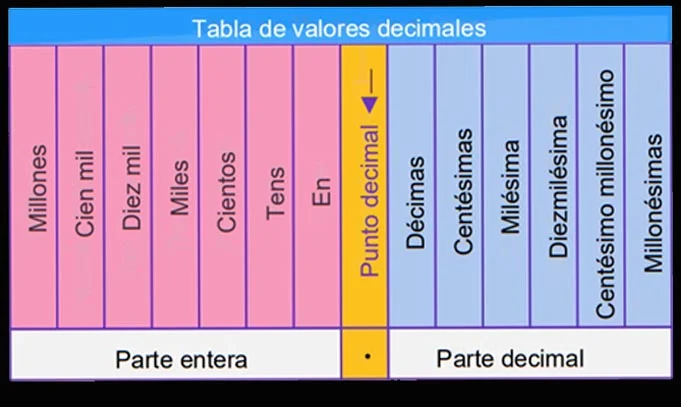
El sistema numérico decimal es sin duda el que nos resulta más familiar. Consta de diez dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Estos diez dígitos constituyen la base para representar todos los demás números. En este sistema, el valor de un dígito dentro de un número depende de su posición. De derecha a izquierda, cada posición representa un valor diez veces mayor que el de su derecha. Esta propiedad fundamental hace del sistema decimal una piedra angular de las matemáticas.
Sistema numérico binario
En marcado contraste con el sistema decimal, el sistema numérico binario emplea sólo dos dígitos: 0 y 1. Esta característica binaria, como su nombre indica, da lugar al término “base 2”. Cada dígito de un número binario se denomina bit, y el número de bits de una representación binaria determina su magnitud. Los números binarios forman parte integrante de los dispositivos electrónicos y los sistemas informáticos, en los que los dos estados “ON” y “OFF” corresponden a 0 y 1. Los ordenadores y los dispositivos digitales utilizan exclusivamente el sistema binario debido a su compatibilidad con los componentes electrónicos.
Ejemplos de números binarios
1011
101010
1101101
En los ejemplos anteriores, podemos ver que cada dígito es 0 ó 1, lo que lo convierte en un método de representación conciso pero potente.
Sistema numérico octal
En el Sistema Numérico Octal, el valor base es 8, y utiliza dígitos del 0 al 7 para su representación. Los números octales pueden convertirse en decimales multiplicando cada dígito por su valor posicional y sumando los resultados.
Sistema numérico hexadecimal
El sistema numérico hexadecimal combina elementos de los sistemas decimal (base 10) y binario (base 2). En hexadecimal, hay dieciséis dígitos únicos, formados por los dígitos 0-9 y las cinco primeras letras del alfabeto (A-F). Este sistema es especialmente útil en informática y programación, ya que proporciona una representación compacta de los datos binarios.
Tabla de sistemas numéricos
| Decimal | Binario | Hexadecimal | Octal |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 8 | 10 |
| 9 | 1001 | 9 | 11 |
| 10 | 1010 | A | 12 |
| 11 | 1011 | B | 13 |
| 12 | 1100 | C | 14 |
| 13 | 1101 | D | 15 |
| 14 | 1110 | E | 16 |
| 15 | 1111 | F | 17 |
| 16 | 10000 | 10 | 20 |
| 17 | 10001 | 11 | 21 |
| 18 | 10010 | 12 | 22 |
| 19 | 10011 | 13 | 23 |
| 20 | 10100 | 14 | 24 |
Conversión entre sistemas numéricos
La conversión entre sistemas numéricos es un proceso sencillo. Cualquier número de un sistema puede convertirse a otro utilizando métodos específicos. Exploremos el proceso de conversión de los sistemas numéricos decimal, binario, octal y hexadecimal.
Conversión de decimal a binario
Los números decimales se representan en base 10, pero los números binarios están en base 2. Por lo tanto, para convertir un número decimal en un número binario, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Divida el número decimal por la base del sistema numérico al que desea convertirlo. Aquí la conversión es a binario, por lo tanto el divisor será 2.
- Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
- Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 2.
- Paso 4: El resto obtenido se convertirá en la segunda cifra menos significativa, es decir, se sumará a la izquierda de la cifra obtenida anteriormente.
Ahora, los pasos 3 y 4 se repiten hasta que el cociente obtenido se convierte en 0, y los restos obtenidos después de cada iteración se añaden a la izquierda de los dígitos existentes.
Una vez finalizadas todas las iteraciones, el último resto obtenido se denominará dígito más significativo.

Conversión de Decimal a Octal
Los números octales se representan en base 8. Por lo tanto, para convertir un número decimal a octal, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Dividir el Número Decimal con la base del sistema numérico al que se desea convertir. Aquí la conversión es a octal, por lo tanto el divisor será 8.
- Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
- Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 8.
- Paso 4: El resto obtenido se convertirá en el segundo dígito menos significativo, es decir, se añadirá a la izquierda del dígito obtenido anteriormente.
Ahora, los pasos 3 y 4 se repiten hasta que el cociente obtenido se convierte en 0, y los restos obtenidos después de cada iteración se añaden a la izquierda de los dígitos existentes.

Conversión de Decimal a Hexadecimal
en los sistemas numéricos Los números hexadecimales se representan en base 16. Por lo tanto, para convertir un número decimal en hexadecimal, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Divida el número decimal por la base del sistema numérico al que desea convertirlo. Aquí la conversión es a hexadecimal, por lo tanto el divisor será 16.
- Paso 2: El resto obtenido de la división se convertirá en el dígito menos significativo del nuevo número.
- Paso 3: El cociente obtenido de la división se convertirá en el siguiente dividendo y se dividirá por la base, es decir, 16.
- Paso 4: El resto obtenido se convertirá en el segundo dígito menos significativo, es decir, se añadirá a la izquierda del dígito obtenido anteriormente.
Ahora, los pasos 3 y 4 se repiten hasta que el cociente obtenido se convierte en 0, y los restos obtenidos después de cada iteración se añaden a la izquierda de los dígitos existentes.

Conversión de sistemas numéricos binarios a otros sistemas numéricos
Los números binarios se representan con los dígitos 0 y 1 y con base 2. La conversión de un sistema numérico significa la conversión de una base a otra. A continuación se muestra la conversión de los sistemas de números binarios a otros sistemas de números:
Conversión de binario a decimal
Los números binarios se representan en base 2, pero los números decimales son de base 10. Por lo tanto, para convertir un número binario en decimal, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Multiplicar cada dígito del número binario por el valor posicional de ese dígito, empezando de derecha a izquierda, es decir, del LSB al MSB.
- Paso 2: Sume el resultado de esta multiplicación y se formará el número decimal.
Ejemplo: Para convertir (11101011)2 en un número decimal

Conversión de Binario a Octal
Los sistemas numéricos binarios se representan en base 2, pero los números octales son de base 8. Por lo tanto, para convertir un número binario en octal, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Divida el número binario en grupos de tres dígitos, empezando de derecha a izquierda, es decir, del LSB al MSB.
- Paso 2: Convierta estos grupos en dígitos octales equivalentes.
Ejemplo: Para convertir (11101011)2 en un número octal

Conversión de Binario a Hexadecimal
Los números binarios se representan en base 2, pero los números hexadecimales están en base 10. Por lo tanto, para convertir un número binario en hexadecimal, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Divida el número binario en grupos de cuatro dígitos, empezando de derecha a izquierda, es decir, del LSB al MSB.
- Paso 2: Convierta estos grupos en dígitos hexadecimales equivalentes.
Ejemplo: Para convertir (1110101101101)2 en un número hexadecimal

Conversión de Sistemas Numéricos Octales a Otros Sistemas Numéricos
Los números octales se representan con los dígitos 0-7 y con base 8. La conversión de un sistema numérico significa la conversión de una base a otra. A continuación se muestran las conversiones de los Sistemas Numéricos Octales a otros Sistemas Numéricos
Conversión Octal a Decimal
Los números octales se representan en base 8, pero los decimales están en base 10. Por lo tanto, para convertir un número octal en un número decimal, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Multiplicar cada dígito del número octal por el valor posicional de ese dígito, empezando de derecha a izquierda, es decir, del LSB al MSB.
- Paso 2: Sume el resultado de esta multiplicación, y se formará el número decimal.

Conversión octal a binario
Los sistemas de números octales se representan en base 8, pero los números binarios están en base 2. Por lo tanto, para convertir un número octal en un número binario, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Escribe cada dígito del número octal por separado.
- Paso 2: Convierte cada dígito en un grupo equivalente de tres dígitos binarios.
- Paso 3: Combine estos grupos para formar el número binario completo.
Ejemplo: (247)8 debe convertirse a binario

Conversión Octal a Hexadecimal
Los sistemas numéricos octales se representan en base 8, pero los hexadecimales son de base 16. Por lo tanto, para convertir un número octal en un número hexadecimal, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Primero tenemos que convertir el número octal a binario. Para ello, siga los pasos dados en la conversión anterior.
- Paso 2: Ahora, para convertir el número binario a hexadecimal, divida los dígitos binarios en grupos de cuatro dígitos empezando de derecha a izquierda, es decir, de LSB a MSB.
- Paso 3: Añadir ceros antes de MSB para que sea un grupo adecuado de cuatro dígitos (si es necesario)
- Paso 4: Ahora convierta estos grupos en sus valores decimales correspondientes.
- Paso 5: Para los valores de 10-15, conviértalos en símbolos hexadecimales, es decir, de la A a la F.
Ejemplo: (5456)8 debe convertirse a hexadecimal

Conversión de Sistemas Numéricos Hexadecimales a Otros Sistemas Numéricos
Los sistemas numéricos hexadecimales se representan con los dígitos 0-9, las letras A-F y la base 16. La conversión de un sistema numérico significa la conversión de una base a otra. A continuación se muestran las conversiones del Sistema Numérico Hexadecimal a otros Sistemas Numéricos
Conversión hexadecimal a decimal
Los sistemas numéricos hexadecimales se representan en base 16, pero los números decimales son de base 10. Por lo tanto, para convertir un número hexadecimal en un número decimal, hay que cambiar la base de ese número. Sigue los pasos que se indican a continuación:
- Paso 1: Escriba los valores decimales de los símbolos utilizados en el número hexadecimal, es decir, de la A a la F.
- Paso 2: Multiplique cada dígito del número hexadecimal por su valor de posición, empezando de derecha a izquierda, es decir, de LSB a MSB.
- Paso 3: Sume el resultado de las multiplicaciones, y la suma final será el número decimal.
Ejemplo: Para convertir (8EB4)16 en un valor decimal

Conversión de hexadecimal a binario
Los números hexadecimales se representan en base 16, pero los números binarios son de base 2. Por lo tanto, para convertir un número hexadecimal en un número binario, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Convertir los símbolos hexadecimales en sus valores decimales equivalentes.
- Paso 2: Escriba cada dígito del número hexadecimal por separado.
- Paso 3: Convierta cada dígito en un grupo equivalente de cuatro dígitos binarios.
- Paso 4: Combina estos grupos para formar el número binario completo.
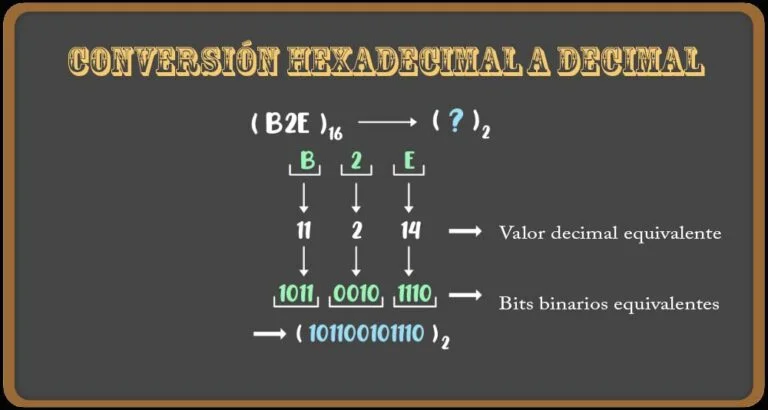
Ejemplo: (B2E)16 debe convertirse a binario
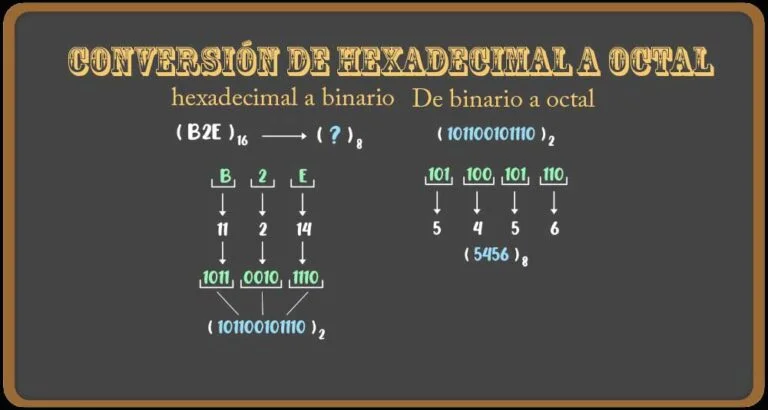
Conversión de Hexadecimal a Octal
Los sistemas numéricos hexadecimales se representan en base 16, pero los octales son de base 8. Por lo tanto, para convertir un número hexadecimal en un número octal, hay que cambiar la base de ese número. Siga los pasos que se indican a continuación:
- Paso 1: Primero tenemos que convertir el número hexadecimal a binario. Para ello, siga los pasos indicados en la conversión anterior.
- Paso 2: Ahora, para convertir el número binario a Octal, divida los dígitos binarios en grupos de tres dígitos empezando de derecha a izquierda, es decir, de LSB a MSB.
- Paso 3: Añadir ceros antes de MSB para que sea un grupo adecuado de tres dígitos (si es necesario)
- Paso 4: Ahora convierta estos grupos en sus valores decimales correspondientes.
Ejemplo: (B2E)16 debe ser convertido a hexadecimal
Conclusión
En esta exhaustiva exploración de los sistemas numéricos, hemos desentrañado los entresijos de los sistemas decimal, binario y hexadecimal. Cada uno de estos sistemas ofrece sus propias ventajas y aplicaciones en diversos campos de las matemáticas y la tecnología. Comprender estos conceptos fundamentales es esencial para cualquiera que desee navegar por el mundo de los números y las operaciones matemáticas con eficacia. Tanto si eres estudiante, educador o una mente curiosa en busca de conocimiento, esta guía te servirá como un valioso recurso en tu viaje matemático.
Tanto si trabaja con sistemas decimales, binarios, octales o hexadecimales, cada uno tiene sus propias características y ventajas en diferentes aplicaciones, lo que los convierte en herramientas indispensables en el mundo de las matemáticas y más allá.

