En el ámbito de los tipos de Números en Matemáticas son los bloques de construcción fundamentales utilizados para cuantificar y representar diversos aspectos del mundo que nos rodea. Los números desempeñan un papel fundamental en tareas tan cotidianas como contar dinero y controlar el tiempo o en conceptos matemáticos complejos. En esta completa guía nos adentramos en el variado mundo de los números, analizando sus definiciones y propiedades y proporcionando ejemplos ilustrativos.
Explorar los principales tipos de números
Hay números de todas las formas y tamaños, cada uno con su propia personalidad. Están los simpáticos números enteros, siempre dispuestos a contar tus manzanas y juguetes. Los decimales, esos artistas de la precisión, se cuelan entre ellos con sus diminutos puntos y fracciones, haciendo de las matemáticas una delicada danza.
Los enigmáticos números primos guardan sus secretos, sólo divisibles por uno y por sí mismos, mientras que los números irracionales, como pi, son eternos y nunca repiten sus dígitos. Y luego están los números complejos, con sus amigos imaginarios, que añaden un toque de magia al reino numérico. De los números enteros a los irracionales, los números son los pilares de nuestro universo matemático, cada uno con su propia historia que espera ser desentrañada.
Números naturales
En tipos de Números 1er número son Los números naturales, a menudo denominados “números de conteo”, engloban el conjunto de números enteros positivos que empiezan por 1 y se extienden hasta el infinito. Estos números se simbolizan con la letra “N” y pueden representarse como:
N = {1, 2, 3, 4, 5, …}
Ejemplos: 35, 59, 110, etc.
Propiedades de los números naturales:
- La suma de números naturales es cerrada, asociativa y conmutativa.
- La multiplicación de números naturales también es cerrada, asociativa y conmutativa.
- El elemento de identidad de la suma es cero.
- El elemento de identidad de la multiplicación es uno.

tipos de números cuando se añade el cero
Cuando se incluye el cero junto con los números naturales, este tipo de números se denominan números enteros. Consisten en números enteros no negativos sin ninguna parte decimal o fraccionaria y se representan con la letra “W”.
W = {0, 1, 2, 3, 4, …}
Ejemplos: 67, 0, 49, 52, etc.
Propiedades de los números enteros:
- Los números enteros son cerrados tanto en la suma como en la multiplicación.
- El cero actúa como elemento aditivo de identidad de los números enteros.
- El uno actúa como elemento de identidad multiplicativa.
- Los números enteros cumplen las propiedades conmutativa y asociativa tanto para la suma como para la multiplicación.
- También cumplen la propiedad distributiva de la multiplicación sobre la suma y viceversa.

Tipos de números enteros
Los números enteros son dos tipos de números; constan de números enteros positivos y números enteros negativos, por lo que los números enteros engloban todos los números enteros, pero también introducen el concepto de números negativos. Se representan con el símbolo “Z”.
Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
Ejemplos: -52, 0, -1, 16, 82, etc.
Propiedades de los números enteros:
- Los números enteros son cerrados bajo suma, resta y multiplicación.
- La propiedad conmutativa se cumple tanto para la suma como para la multiplicación de enteros.
- Los números enteros siguen la propiedad asociativa tanto para la suma como para la multiplicación.
- Cumplen la propiedad distributiva tanto para la suma como para la multiplicación.
- La identidad aditiva de los números enteros es 0, mientras que la identidad multiplicativa es 1.
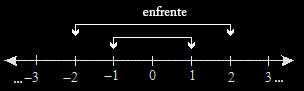
En matemáticas, la recta numérica es una forma de representar números en una línea recta para leer más sobre las rectas numéricas ve a esta página.
Tipos de números reales
cuando se combinan distintos tipos de números forman Los números reales abarcan una amplia gama de números, incluidos los enteros positivos y negativos, las fracciones y los números decimales, excluidos los números imaginarios. Se representan con la letra “R”:
Ejemplos: 3/4, 0,333, √2, 0, -10, 20, etc.
Propiedades de los números reales:
- Los números reales son conmutativos, asociativos y distributivos tanto en la suma como en la multiplicación.
- Obedecen a la propiedad inversa.
- Los elementos de identidad aditiva y multiplicativa de los números reales son 0 y 1, respectivamente.
Números racionales
Los números racionales son aquel tipo de números que se pueden expresar en la forma p/q, donde p y q son números enteros, y q no es igual a cero. Se representan con la letra “Q”:
Ejemplos: 7/1, 10/2, 1/1, 0/1, etc.
Propiedades de los números racionales:
- Los números racionales son cerrados bajo suma, resta, multiplicación y división.
- Satisfacen las propiedades conmutativa y asociativa bajo suma y multiplicación.
- Los números racionales cumplen la propiedad distributiva en la suma y la resta.
Números irracionales
Los números racionales son aquellos tipos de números que no pueden expresarse como cociente de dos enteros. Incluyen números como √2, π y la constante de Euler.
Ejemplos: √2, π, constante de Euler, etc.
Propiedades de los números irracionales:
- Los números irracionales no satisfacen la propiedad de cierre.
- Obedecen a propiedades conmutativas y asociativas bajo suma y multiplicación.
- Los números irracionales son distributivos en la suma y la resta.
Números complejos
Los números complejos se expresan en la forma a+bi, donde “a” y “b” son números reales, e “i” representa la unidad imaginaria. Algunos ejemplos son 4 + 4i, -2 + 3i y 1 + √2i.
Propiedades de los números complejos:
- Los números complejos siguen las propiedades asociativa y conmutativa de la suma y la multiplicación.
- También se adhieren a la propiedad distributiva de la multiplicación sobre la suma.
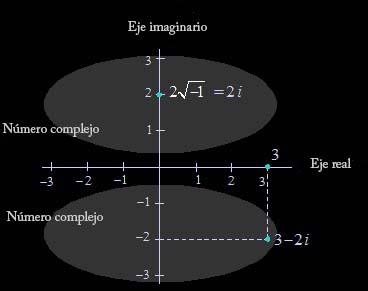
Tipos de números imaginarios
Los números imaginarios son un subconjunto de los números complejos que implican múltiplos de la unidad imaginaria “i”. Presentan una propiedad única: al multiplicarlos por “i”, pasan por cuatro valores diferentes:
1 × i = i
i × i = -1
-1 × i = -i
-i × i = 1
Así pues, los números imaginarios pueden escribirse como
i = √1
2i = -1
3i = -i
4i = 1
4ni = 1
(Donde “n” es un número entero)
Conclusión
En conclusión, comprender los distintos tipos de números en matemáticas es crucial para una base sólida en conceptos matemáticos. Cada categoría de números tiene sus propias propiedades y aplicaciones, que contribuyen a la riqueza del conocimiento matemático.

